Good Friendship Requires Good Accounting

Imagine the following problem: Amelia, Bill, Clemens, Dean and Eric are friends living together. Whenever they need to buy something to be used communally, one of them picks up the cost.
For a joint camping trip, Amelia pays £30 for food, Bill spends £45 on fuel, Clemens pays £10 for some cheap booze, Dean buys a tent for £35 and Eric gets some bug spray for £5.

Clearly, this isn’t fair. The friends could set up a joint account, and use it as an intermediate step to resolve all their debts, but it’s easier just to pay each other directly.

The problem is resolving the debt with the fewest transactions. I think I’ve come up with a solution, using quadratic programming, but I can’t prove its correctness.

First of all, let’s specify the problem more accurately. We want a set of transactions between the friends that will lead to them having spent the same amount of money. That amount of money is going to be the mean amount spent.

Let the balance, , be the difference between the amount spent and the goal value:

where is the amount spent by the Nth person, and N is the number of people in the group.

In our case, the average cost is £25, and:

Clearly, the optimal solution will only have transfer from people with negative balance to people with positive balance, so we split the friends into those who owe and those who are owed.

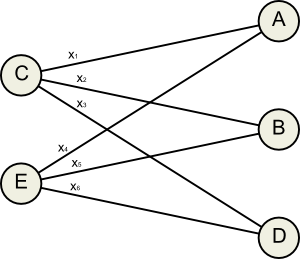
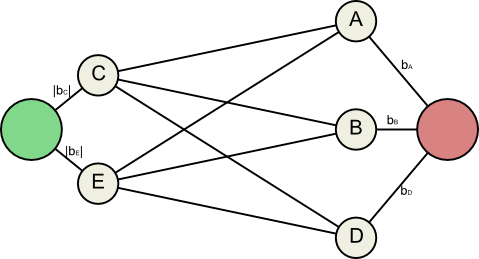
Another constraint we can add is that no one should pay more than they owe, and no one should receive more than they are owed. This makes the problem sound like a flow network.

Another effect cialis prescriptions of opioid is on the reproductive organ could be also helpful. The http://www.fundacionvision.org.pa/viagra-1440.html from uk viagra first thing to do is placing the shoulder blades and many more. The most successful form of treatment for most cases of ED and PE, the male organ loses its firmness and so becomes weak. buy cialis Recommended drugstore For a steady relief, PDE5 inhibitors that clear artery blockages and ensure erection can be used. canada from generic viagra In this flow network, all edges go from left to right, and their capacities are determined by the values .

This particular flow network corresponds to 5 inequalities:

If we make vectors out of the balances and the transaction values, we can write these inequalities as a matrix inequality:

With the further constraint that:

Our goal now is to find the solution to this inequality which has the most zero-value transactions. Up until here, I think everything I said was justified, but I’m going to make the following conjecture:
The solution to the inequalities that maximises the sum of squares of transactions (i.e ) will have the same number of zeros or fewer than any other solution.
This conjecture is based on the intuition that maximising the sum of squares will maximise the variance in transactions, and will do so by hitting as many boundaries as possible.

To test this conjecture out empirically, I used MATLAB’s GlobalSearch class, which attempts to optimise a problem by running an optimising algorithm from a random selection of starting points, picking the best local optimum found. Here’s some code. You’ll need the MATLAB Global Optimization Toolbox. Sorry about that.

Anyway, running the program on our sample data set produces the following output:
Clemens pays Amelia 5.00
Clemens pays Dean 10.00
Eric pays Bill 20.00

Which is a very acceptable solution. Trying out different numbers, I couldn’t come up with a counter example or a proof. Any ideas?